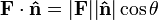NOTACION
Un vector unitario se denota frecuentemente con un acento circunflejo sobre su nombre, como  (se lee "r vector" o "vector r"). La notación mediante el uso de una breve () también es común, especialmente en desarrollos manuscritos. La tendencia actual es representar el vector en la dirección del vector  en la forma .

DEFINICION

Habiendo definido el concepto de vector unitario al comienzo de este artículo y habiendo presentado la notación usual en la sección anterior, presentamos en esta sección una definición simbólica de vector unitario.

Sea el vector v ∈ ℝⁿ. Se dice que v es un vector unitario y se lo denota mediante  si y solamente si el módulo de v es igual a 1.

O en forma más compacta:

PRODUCTO ESCALAR DE DOS VECTORES

En el espacio euclídeo, el producto escalar de dos vectores unitarios es simplemente el coseno del ángulo entre ellos. Esto es consecuencia de la definición de producto escalar y del hecho de que el módulo de ambos vectores es la unidad:

Pero:

Por lo tanto:

donde θ es el ángulo entre ambos vectores.

Proyección escalar[editar]

De lo anterior, resulta que el producto de un vector por un vector (o vector unitario) es la proyección escalar del vector sobre la dirección determinada por el vector.

Como el módulo del vector  es la unidad, la ecuación anterior se transforma en:

de donde es evidente lo afirmado al comienzo de este apartado. Este resultado es muy frecuente en física, donde en necesario operar, por ejemplo, con las componentes ortogonales a una superficie.